增长率专题

🌐 6076 字 ⌛ 23 分钟

增长率可以简写成 r，增长率表示两者变化的相对量

增长率公式

增长率 ＝ $\frac{{\mathrm{增长量}}^{}}{\mathrm{基期量}}$ ＝ $\frac{{\mathrm{增长量}}^{}}{\mathrm{现期量\; -\; 增长量}}$ ＝ $\frac{{\mathrm{现期量\; -\; 基期量}}^{}}{\mathrm{基期量}}$ ＝ $\frac{{\mathrm{现期量}}^{}}{\mathrm{基期量}}$ - 1

增长率别称

增长率又称增速、增幅或者增长速度、增长幅度、增值率等

负增长率

增长率为负数时表示下降，下降率也可以直接写成负的增长率

例：（2024国家）

2023年1~3月我国机器人设备累计出口金额1.9亿美元，较上年增长62.1%，累计进口金额6.9亿美元，较上年增长55.1%。 问：2023年一季度，我国机器人设备进出口贸易逆差比上年同期：

A.下降了不到30%

B.下降了30%以上

C.上升了不到30%

D.上升了30%以上

详解

解析内容

一、增幅、降幅、变化幅度

1. 增幅（增长率/增速）：可正可负，比较时要带正负号（5% ＞ -10%）

2. 降幅：增长率为负，比较时看绝对值（|-5%| ＜ |-10%|）

3. 变化幅度：增长率可正可负，比较时看绝对值（|5%| ＜ |-10%|）

4. 求增长率方法

（1）出现增速

 ① 2024年收入10万元，同比增长10%，增速比去年提高5个百分点。则2023年的增长率为： 

 ② 2024年收入10万元，同比增长10%，增速比去年回落5个百分点。则2023年的增长率为： 

 `分析：`“增速”直接带符号，用“高减低加”。
 ① 10%-5%=5%，所以2023年的增长率为5%。② 10%+5%=15%，所以2023年的增长率为15%。

（2）出现降幅

 ① 2024年收入10万元，同比下降10%，降幅比去年扩大5个百分点。则2023年的增长率为：  

 ② 2024年收入10万元，同比下降10%，降幅比去年收窄5个百分点。则2023年的增长率为：  

 `分析：`“降幅”先不带符号用“高减低加”，后面再添“负号”。
 ① 10%-5%=5%，添负号后2023年的增长率为-5%。② 10%+5%=15%，添负号后2023年的增长率为-15%。

---

二、百分数与百分点

1. 百分数：表示两个量的比例关系，用除法计算

   例：2022年为150，21年为100，则22年比21年增长$\frac{150-100}{100}$ = 50%

2. 百分点：表示百分数的变化，用加减法计算

   例：22年为70%，21年为20%，则22年比21年增长 70 - 20 = 50 个百分点

3. 考察形式：给出一个百分数和百分点，求另一个百分数

   例：22年为70%，比21年提高了20个百分点，则21年为 50%

   例：22年为70%，比21年降低了20个百分点，则21年为 90%

---

三、增长率比较

1. 题型识别：增长率/增速/增幅最大或最小；增长+最快或最慢。

2. 公式：增长率 ＝ $\frac{{\mathrm{增长量}}^{}}{\mathrm{基期量}}$ ＝ $\frac{{\mathrm{现期量\; -\; 基期量}}^{}}{\mathrm{基期量}}$ ＝ $\frac{{\mathrm{现期量}}^{}}{\mathrm{基期量}}$ - 1

3. 题型分类：

   （1）“已知现期、基期”型：

   ① 倍数明显，直接比较 $\frac{{\mathrm{现期}}^{}}{\mathrm{基期}}$

   ② 倍数不明显或现期与基期差距小用 $\frac{{\mathrm{增长量}}^{}}{\mathrm{基期}}$

   ③ 若基期量很接近时，可以直接用增长量作比较。

   （2）“已知现期、增长量”型：直接比较 $\frac{{\mathrm{增长量}}^{}}{\mathrm{现期}}$

   原理：增长率 ＝ 增长量 ÷（现期量-增长量）＝ $\frac{1^{}}{\mathrm{现期量\; ÷\; 增长量\; -\; 1}}$，因为增长率与现期量 ÷ 增长量成反比，所以增长率与增长量 ÷ 现期量成正比。

例：（2015贵州）

2012年末，中国大陆总人口135404万人，全年出生人口1635万人，死亡人口966万人。从性别结构看，男性人口69395万人，同比增加327万人，女性人口66009万人，同比增加342万人；从城乡结构看，城镇人口71182万人，同比增加2103万人；乡村人口64222万人，同比减少1434万人。 问：2012年中国男性人口、女性人口、城镇人口的同比增长率按大小排序正确地是：（ ）

A.城镇人口>男性人口>女性人口

B.城镇人口>女性人口>男性人口

C.女性人口>男性人口>城镇人口

D.女性人口>城镇人口>男性人口

详解

解析内容

例：（2024甘肃）

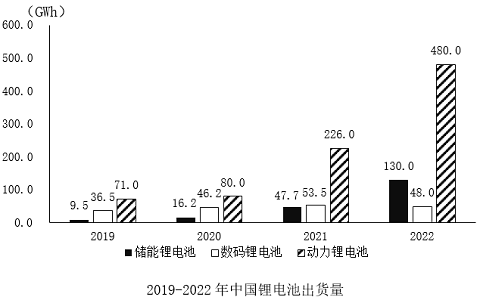问：以下锂电池出货量指标中同比增速最快的是：

A.2021年储能锂电池出货量

B.2021年动力锂电池出货量

C.2022年储能锂电池出货量

D.2022年动力锂电池出货量

详解

解析内容

四、间隔增长率

1. 题型识别：中间隔一个时期（一般隔1年），求增长率。例如有三个时期2022、2023、2024，已知2023与2022相比较的增长率为$r_1$，2024与2023比较的增长率为$r_2$。求2024与2022相比较的增长率$r$，这种题型称为间隔增长率。

2. 公式：$r = r_1 + r_2 + r_1 \times r_2$

3. 公式推导：
   设2022年量为1，则2023量为$1 + r_1$，知道基期及增长率，根据现期公式（基期+(基期×增长率)）则2023量为1+(1×r_1)=1+r_1，2024年量为$(1 + r_1)(1 + r_2) = 1 + r_1 + r_2 + r_1 \times r_2$，则2024年与2022年比较的增长率 r = $\frac{{\mathrm{现期-基期}}^{}}{\mathrm{基期}}$ = $\frac{(1 + r_1 + r_2 + r_1 \times r_2) - 1}{1} = r_1 + r_2 + r_1 \times r_2$

4. 速算技巧：

   （1）先算加法$r_1 + r_2$，排除选项

   （2）如果$r_1$和$r_2$均小于10%，可忽略乘法。示例：5%+8%+5%×8%≈？由于5%、8%均小于10%，可以忽略$r_1$ × $r_2$，则原式≈5%+8%=13%。

   （3）如果$r_1$或$r_2$大于10%，其中一个百分化。示例：5%+36%+5%×36%≈？由于36%>10%，$r_1$ × $r_2$ 不能忽略。可以将5%化成分数为1/20，然后计算36%/20=1.8%，则原式≈41%+1.8%=42.8%。

例：（2017国家）

2015年全行业全年生产手表10.7亿只，同比增长3.9%，完成产值约417亿元，同比增长4.3%，增速提高1.9个百分点；生产时钟(含钟心)5.2亿只，同比下降3.7%，完成产值162亿元，同比下降4.7%，降幅扩大1.3个百分点 问：2015年我国钟表全行业生产时钟(含钟心)的产值与2013年相比约( )

A.上升了11%

B.下降了11%

C.上升了8%

D.下降了8%

详解

解析内容

五、乘积增长率

1. 定义：即量之间满足C＝B×A形式时，已知$r_a$，$r_b$，求$C$的增长率$r_c$，即$C$的增长率称为乘积增长率。

2. 公式：$r_c = r_a + r_b + r_a \times r_b$ (与间隔增长率公式一样)

3. 常用题型：

   （1）平均数类问题，总数＝平均数×个数，求解总数的增长率时

   （2）比重类问题，部分量＝整体量×比重，求解部分量的增长率时

   （3）经济利润问题，总价＝单价×数量，求解总价的增长率时

4. 公式推导：

   例如：单位面积产量(A)的增长率为$a$，面积(B)的增长率为$b$，求总产量的增长率$c$？

（1）其中：总产量=(A)单位面积产量×(B)面积

（2）总产量增长率公式(c) = $\frac{{\mathrm{总产量现期-总产量基期}}^{}}{\mathrm{总产量基期}}$

（3）总产量现期=A×B，总产量基期=单位面积产量基期×面积基期= $\frac{A}{1+a}$ × $\frac{B}{1+b}$

（4）带入值总产量增长率公式，即：c = $\frac{A*B-\frac{A}{1+a}*\frac{B}{1+b}}{\frac{A}{1+a}*\frac{B}{1+b}}$

（5）化简：c = A × B × $\frac{(1+a)*(1+b)}{A*B}$ - 1 = a ＋ b＋ a × b

例：（2019辽宁）

2019年1—8月，房地产开发企业土地购置面积12236万平方米，同比下降25.6%,每平方米土地价格同比上涨4.5%，土地成交额6374亿元。
问：2019年1—8月，房地产开发企业土地成交额与去年同期相比增长约为：

A.-17%

B.-22%

C.-27%

D.1.2%

详解

解析内容

六、混合增长率

定义：混合增长率的关键在于“混合”，混合即为不同事物交叉混合在一起，那么混合增长率也就是混合后所形成的整体量的增长率，如全班人男人+女人，那么全班人就是男人和女人混合后所形成的整体量，男人和女人为两个部分量，则全班人的增长率就是整体量的增长率，也可称之为混合增长率。

1. 举例：一杯100g含盐量为20%的盐水，和50g清水(含盐量为0%)，混合后含盐量在0%-20%范围内，且偏向于量大的一方。即混合后的增长率处于部分增长率之间，且偏向于基期量大的一方。

2. 题型：部分混合得到整体，求整体增长率（进出口、城镇乡村全国、男女、房地产、1~N月、季度全年半年、油料和水果、A与非A等）

3. 公式：$\frac{{\mathrm{部分基期A}}^{}}{\mathrm{部分基期B}}$ = $\frac{a - c}{c - b}$ 【$a$，$b$为部分增长率，$c$为整体增长率】

4. 做题技巧：

   （1）混合后的放中间，混合前的放两边（b < 混合r < a）

   （2）先求两者增长率平均值$\frac{a+b}{2}$，然后看谁基期量大（一般可以拿现期代替基期），混合后的增长率就往谁靠。如果现期量接近，增长率一正一负或增长率差距非常大时，要用基期量。一般这一步可以排除2~3个选项。

   （3）使用公式准确计算。

5. 计算方法：

   （1）十字交叉法

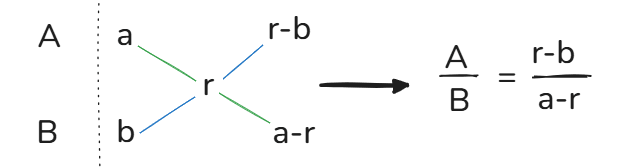   a，b为部分增长率，r为混合增长率，A，B为基期

   口诀：整体增长率写中间，部分增长率写左边（大的在上，小的在下），交叉做差，得到基期之比。（增长率差距小时可以用现期代替基期）

   （2）线段法

   

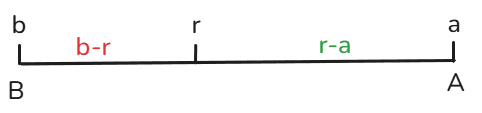
   口诀：部分增长率写两边，整体增长率写中间，距离和基期成反比。距离是指混合后的距离的两端差。（增长率差距小时可以用现期代替基期）

6. 公式推导：

定义部分和整体的基期量和对应增长率：

基期量	对应增长率
部分A基期量	$r_a$
部分B基期量	$r_b$
整体基期量(Z)	$r_z$

部分基期之和=整体基期，部分增长量之和=整体的增长量
整体基期：$Z = A + B$

整体增长量：$Z \times r_z = A \times r_a + B \times r_b$

将整体基期公式①代入整体增长量公式②右侧，则有：$A \times r_a + B \times r_b$ = $Z \times r_z$ = $(A + B) \times r_z$ = $A \times r_z + B \times r_z$

移向得：$A \times r_a + A \times r_z = B \times r_z - B \times r_b$

提取公因数得：$A \times (r_a + r_z) = B \times (r_z - r_b)$

则有：$\frac{A}{B}$ = $\frac{r_z-r_b}{r_a-r_z}$

例：（2019国家）

2017年，A省完成邮电业务总量6065.71亿元。其中，电信业务总量3575.86亿元，同比增长75.8%;邮政业务总量2489.85亿元，增长32.0%。问：2017年A省邮电业务总量同比增速在以下哪个范围之内?

A.低于25%

B.25%～50%之间

C.50%～75%之间

D.超过75%

详解

解析内容

七、年均增长率

定义：年均增长率是统计学中的一个概念，也被称为复合增长率。它表示在一定年限内，平均每年增长的速度。

1. 题型识别：年均 + 增长 + %

2. 公式：$(1 + r)^n$ = $\frac{{\mathrm{现期}}^{}}{\mathrm{基期}}$（$n$=年份差，$r$为年均增长率）

3. 估算公式：年均增长率 ≤（$\frac{{\mathrm{现期}}^{}}{\mathrm{基期}}$ - 1）÷$n$，利用这个估算公式可以排除答案。

4. 年均增长率比较：年份$n$相同，直接比较

5. 年份差的计算：年份差 = 尾年 - 首年。如2016~2020年，年份差是4年。

   （1）五年规划年份差为5，如十三五(2016-2020年)，基期是2015年，现期是2020年

   （2）如果题目说明了这N年，则年份差为N，如2016-2020年这5年，基期是2015年

   （3）江苏省考：基期需要往前推一年。如2010年~2014年间的年均增量，年份差为5，基期是2009年

6. 速算技巧一：72/115法则（选项差距较大时使用）

   定义：当现期÷基期=2时，r ≈ 72% / n；当现期÷基期=3时，r ≈ 115% / n。（$n$为年份差）

   例子：$18(1+r)^ 4=37$，37/18≈2.06，72/4≈18，所以r≈18%

   修正表(A/B)	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
   nr近似值	10	19	27	35	42	49	63	72	100

7. 速算技巧二：二项式展开+修正

公式： $(1+r)^n$ = 1 + $C_{n}^{1}$r + $C_{n}^{2}$r² + ... + $C_{n}^{n}$rⁿ，其中（$C_{n}^{n}$ = 1）

计算方法：当年均增长率≤5%时，取前两项，$\frac{{\mathrm{现期\; ÷\; 基期\; -\; 1}}^{}}{\mathrm{n}}$，结果需修正（偏小）

修正：计算的时候后面很多项没有取，结果取小了，r算大了，那么结果要选偏小的。具体大多少？假设我们计算的年均增长率为Q，粗略估算偏大Q²，实际结果选Q-Q²。修正并不是准确值，还是存在误差，当Q较大时不适用。 如果不想修正，那取前面三项，则$(1+r)^n$ ≈ 1 + $C_{n}^{1}$r + $C_{n}^{2}$r² = 1 + nr + $\frac{n(n-1)}{2}$$r^2$

建议：一般无论年均增长率是否小于5%，很多时候做题取前面两项计算再修正可以得出答案。 例如：2007年89147，2003年49788，求2003~2007年均增长率？【A：10%；B：16%；C：25%】

分析：年份差n=4，利用r $\frac{{\mathrm{现期\; ÷\; 基期\; -\; 1}}^{}}{\mathrm{n}}$= $\frac{{\mathrm{现期\; ÷\; 基期\; -\; 1}}^{}}{\mathrm{n}}$ =((9÷5)-1)÷4≈20%；答案选不出来，进行修正，r=20%-20%×20%=16%。选C。如果不修正，取前面三项：现期÷基期=1+4r+6r²，则1.8=1+4r+6r²，则0.4=2r+3r²，根据选项代入20%，发现2r就等于0.4了，说明r大了，代入10%，2r+3r²明显小于0.4，则20%>年均增长率>10%。选C。

8. 速算技巧三：代入法

   ① 记忆常见多次方数；

   ② 代入中间值或表格特殊值

   （1+r）ⁿ	2次方	3次方	4次方	5次方
   1.1	1.21	1.33	1.46	1.61
   1.15	1.32	1.52	1.75	2.01
   1.2	1.44	1.73	2.07	2.49
   1.25	1.56	1.95	2.44	3.05
   1.3	1.69	2.2	2.86	3.71
   1.35	1.82	2.46	3.32	4.48
   1.4	1.96	2.74	3.84	5.38

速算总结：

①72/115法则，建议选项差距较大时使用。

②二项式展开，取两项+修正建议年均增长率较小时使用；取三项，这个比较准确，但计算量大，不建议。

③代入法，个人推荐，根据选项假设一个中间的、好计算的增长率代入公式计算或者直接代入选项，可以排除掉两个答案，重复两遍可得到正确答案。

④编数法，源自齐麟，网上很火的方法，个人感觉很麻烦并且计算量稍大，想了解的可以在网络搜一下。原理就是 平均增长率≈年均增长率。假如求2016~2020年均增长率，其实公式并没有涉及2017、2018、2019相关的数，那么给这三个年份编一个容易计算的数据，计算每年的增长率，再求平均。

例：（2018上海）

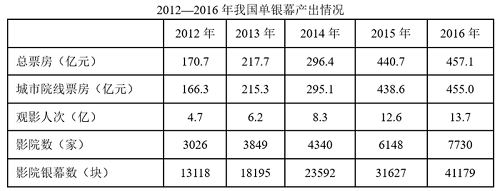问：2012-2016年，我国单银幕总票房平均每年较上年增长约：

A.13%

B.28%

C.54%

D.67%

详解

解析内容

八、平均数增长率

定义：平均数的增长率，要同时体现平均数、增长率两层含义。比如2021年人均收入比去年增加了百分之多少。

题型识别：平均数+增长了...

公式：$r = \frac{a - b}{1 + b}$，其中$a$表示平均数中分子的增长率，$b$表示平均数中分母的增长率。

公式推导：
现期的平均数为 $\frac{{\mathrm{个数}}^{}}{\mathrm{总数}}$，我们用$\frac{A}{B}$表示，A的增长率为a，B的增长率为b

则基期的平均数为 $\frac{A}{B}$ × $\frac{1+b}{1+a}$

带入增长率公式 $\frac{{\mathrm{现期平均数}}^{}}{\mathrm{基期平均数}}$ -1，即 [$\frac{A}{B} \div (\frac{A}{B} \times \frac{1+b}{1+a})$] - 1

化简可得增长率：$\frac{1+a}{1+b}$ - 1 = $\frac{a-b}{a+b}$

如果求“现期平均数是基期平均数的多少倍”，倍数 = 增长率 + 1 = $\frac{a-b}{1+b}$ + 1

计算：

（1）计算分子a-b

 ① 当a - b > 0，现期平均数同比上升  

 ② 当a - b < 0，现期平均数同比下降

（2）再看b符号

 ① 当b > 0，分母（1+b）>1，结果的绝对值<|a-b|  

 ② 当b < 0，分母（1+b）<1，结果的绝对值>|a-b|

拓展：该公式可用于求$\frac{A}{B}$类型的增长率，如单价= $\frac{{\mathrm{总价}}^{}}{\mathrm{数量}}$的增长率。

例

2016年全国餐饮收入35799亿元，同比增长10.8%，餐饮收入占社会消费品零售总额的比重为10.8%。2016年全社会餐饮业经营单位为365.5万个，同比下降8.2%；从业人数为1846.0万人，同比增长5.7%。问：2016年全社会餐饮业平均每个经营单位的从业人数比上年约：（ ）

A.减少了2%

B.减少了15%

C.增加了2%

D.增加了15%

详解

解析内容

例：