Appearance
数量规律(例题待补充)
考查频次: 它可以单一考点命题,也可以两个考点结合命题(如面和线结合的考法),还可以和其他规律结合命题(如数量规律和属性规律的复合考法)
题型特征:图形元素组成不同
解题思路:当图形元素组成不同时,常考查属性、数量及其他特殊规律。当题干图形无明显属性规律时,可优先考虑数量规律。常考的数量规律有五种: 图形元素组成不同,且无明显属性规律。
一、点数量
在图形推理中,
即由相切关系得到的交点,如图5,共有 3个交点,其中有2个点为切点。
(注意:切点是交点,交点不一定是切点)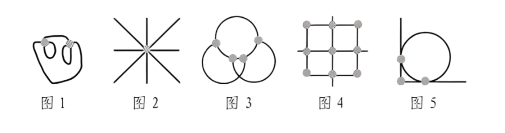
当有以下特征图时,可能考察点的数量规律
- 线条交叉明显(比如米字形)
- 绕来绕去的一团线
- 切点(或顶点)较多
注意考察点的形式:
数点情况:
- 整体数点:
- 交点的数量成等差数列
- 交点的数量无序,但是可以排成有序。比如题干给四幅图,前四幅图的交点数量分别为3、1、5、2;即答案选择4个交点的,排成有序。
- 局部数点:内部和外部交点;内部线条与外框的交点。
- 整体数点:
二、线数量
当有以下特征图时,可能考察线的数量规律:
- 如果图形出现的,可以优先考虑数的数量;
- 如果图形出现的,可以优先考虑数的数量;
- 如果图形出现半曲半直图形,注意;
注意:
- 线出现明显拐点,是2条线。否则算1条。
- 3+2类型题目,可能会考察线的数量求和为定值。
- 九宫格可能会考察:①线的数量求和为定值;②每行或每列线的数量求和呈等差。
- 出现曲线和直线:曲线数、直线数、曲线直线求和或作差
- 注意平行线(图形特点:轮廓自带平行线;N字型、Z字型、工字型、H字型):①考察平行线的组数;②平行线的方向。
三、面
面数量
- 面:也称封闭空间、封闭区域,或者更形象地说就是“窟窿”。注意黑色不是面。
- 数面的特征图:①图形被分割;②封闭区域明显;③生活化图形。
- 注意:如果同时出现数面、数线、数笔画、数点的特征图,优先数面
特殊面
- 面的形状特征:
- 下面图1的面都是三角形,图2的面都是四边形。
- 特别明显的大面或小面,我们可以将其勾画出来进行对比。下面图3的最大面是三角形,图4的最大面是四边形。考点:
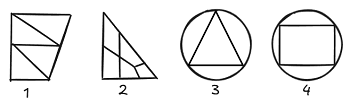
- 面的形状特征:
面的数量复合
- 可能考察面数量和外框边数(是否相等、求和、求差)。
- 面数量和交点数。
- 存在相同面。考察个数、组数。
四、角
角数量
- 角还可以细分为锐角、直角和钝角。
- 扇形、多边形故意留缺口也可以看作角、优先考虑数角。
- 图形中出现直角时(H、工、T 字型的修正和相似图形,电话卡图形),可。
角的特殊考法
- 外框直角数:内部凌乱或有图形没内部,则看外框,考虑外框的线条、外框的角数
- 直角复合旋转:直角数量复合角度旋转。
- 角与元素标记复合:元素标记的角(锐角、直角、钝角)。
五、元素(部分)数量
元素,可细分为。
图1,元素的个数是5,元素种类数是3(正方形、五角星、圆),部分数是5;
图2,元素的个数是5,元素种类数是4(正方形、五角星、圆、桃心),部分数是5
图3,元素的个数是3,元素种类数是3(五角星、四角星、椭圆),因为这三种小元素都连在了一起,因此部分数是1

当图形由很多可以数元素的个数、种类;
题目特点:
- 元素凌乱
- 多个小图形或多个线条
- 加粗黑体
六、笔画
题型:
笔画数的特征图:
五角星、“日”字及其变形、“田”字及其变形、多圆相切、多圆相交以及出现大量端点时,优先考虑笔画数。
判断图形的笔画:对于简单图形,可通过临摹的方式直接得出,而对于复杂图形,可通过下列公式进行计算:连通图的其中含 0 个奇点的连通图可一笔画完成。
连通图:如果图中任意两点都是连通的,那么该图被称作连通图。这一概念很专业,实际做题时,可大致理解为图形中的线条连在了一起。
奇点:若以一个点为起点,延伸出的线条数为偶数,则该点为偶点。
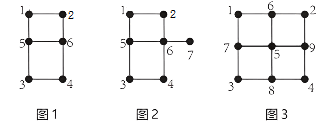
- ,以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶数条,因此它们均为偶点;以点 5、6 为起点,延伸出来的线都是 3 条,奇数条,因此它们均为奇点。图 1 奇点数为 2,可以一笔画完成
- ,以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶数条,因此它们均为偶点;以点 6 为起点,延伸出来的线为 4 条,偶点;以点 5 为起点,延伸出来的线为 3 条,奇点;以点 7 为起点,延伸出来的线为 1 条,奇点。图 2 奇点数为 2,可以一笔画完成。
- ,以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶点;以点 5 为起点,延伸出来的线为 4 条,偶点;以点 6、7、8、9 为起点,延伸出来的线为 3 条,奇点。图 3 奇点数为 4 个,笔画数 =4÷2=2,故须两笔画才能完成
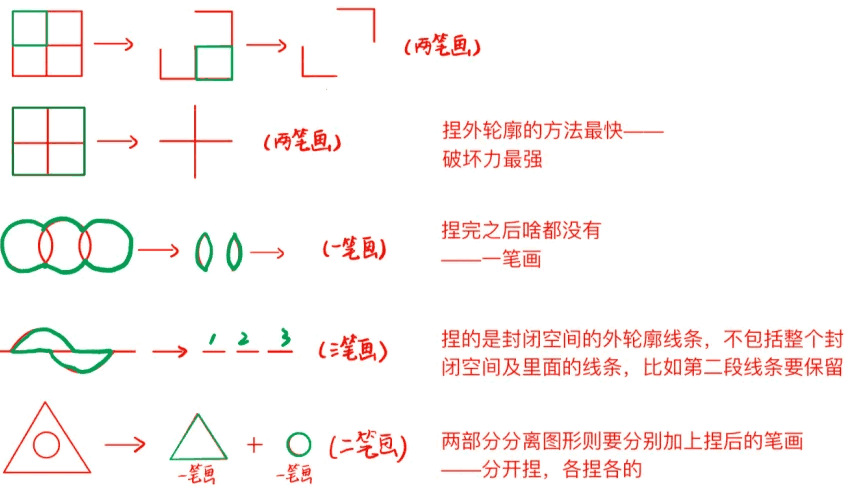
简化一笔画判断之吹捏法:在图形复杂性增加时,数奇点会变得繁琐且耗时。而吹捏法完全摒弃了这一步骤,只需通过简单的铅笔画,即可迅速得出答案。
- 吹捏法步骤:先识别并“捏掉”图形中的所有封闭面,直到只剩下线条连接点。注意多部分分离图形单独捏,最后分别加上捏后的笔画。
- 分析剩余结构:①如果剩余部分为空或仅剩一个点,则原图形为0笔画或1笔画。②如果剩余线条为一条连续线,则图形为一笔画;若为多条分离线条,则笔画数为线条数之和。 该方法不适用于所有图形,例如,当图形无封闭区域或剩余线条结构复杂时。