空间类(例题待补充)

一、六面体

六面体常见展开图

（一）相对面

定义：
在平面展开图中，相对面的基本判定法则：
- 方法一：在平面展开图中，如下图所示，a 面和 f 面、b 面和 d 面、c 面和 e 面均是在同一行或同一列，且中间隔了一个面，所以这 3 组就是相对面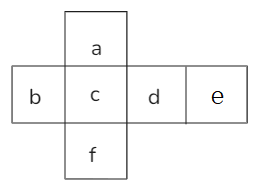
- 方法二：在平面展开图中，如下图所示，三幅图的 a 面和 b 面都是在“Z”字形两端，且紧靠着“Z”字形中间那条线，所以它们都是相对面。注意图 3 的 c 面和 d 面虽然也在“Z”字形两端，但没有紧靠着“Z”字形中间那条竖线，所以不是相对面。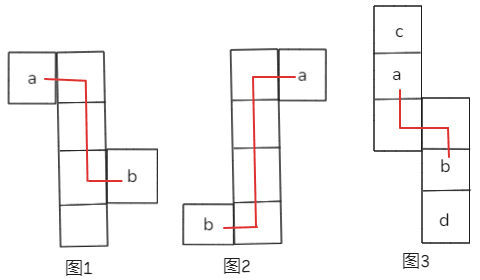
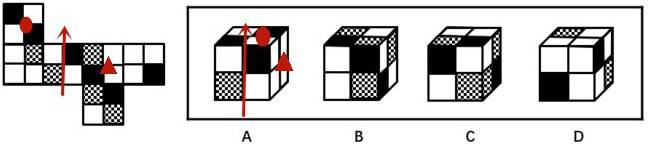
例：（2016 江苏）上边这个图形是由下边四个图形中的某一个作为外表面折叠而成，请指出它是哪一个？

（二）相邻面

相邻面法又分为公共边和公共点，我们先来说说公共边。

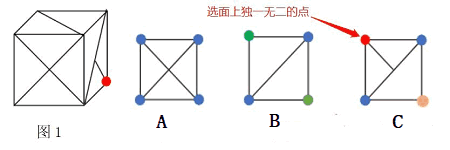
公共边法
- 如图一所示，面 A 和面 B 直接挨在一起，所以面 A 和面 B 是相邻面，中间标红的边是二者的公共边。面 A 和面 C 没有紧挨着，但两条蓝边互相垂直，折叠后可知两条蓝边重合，所以面 A 和面 C 是相邻面。
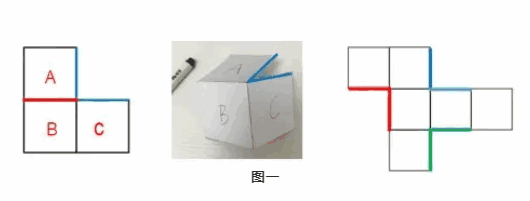
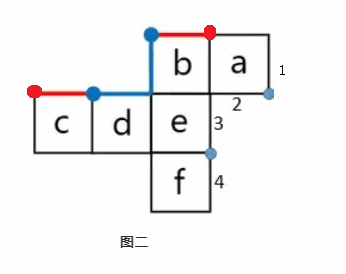
- 如图二所示。 ①面 b 的左边和面 d 的上边呈直角，两条蓝边是同一条边。面 b、面 e、面 d、面 c 呈 “L” 型，面 b 和面 c 是 “L” 型两端的面，因为两条蓝边是同一条边，且两个蓝点是同一个点（找到面 b 和面 d 垂直的边、重合的点），所以这两个蓝点往外延伸出的两条红边也是同一条边。
  ②同理面 a 和面 f 在右侧“L”型的两端，边 2 和边 3 互相垂直，是同一条边，边 2 和边 3 上的两个蓝点是同一个点，由这两个蓝点往外发散出的两条边是同一条边，即边 1 和边 4。
  ③如果听不懂可以先记下来，考试不考查原理，可以之后在做题中慢慢了解。
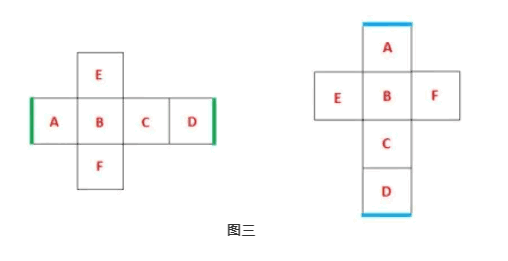
- 如图三所示。
公共点法
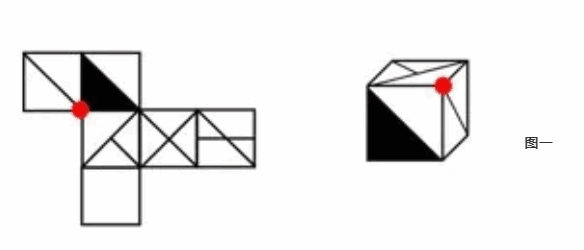
- 如图一所示。展开图的公共点相交黑色直角三角形的直角顶点，而立体图的公共点与黑色直角三角形不相交，所以二者不一致；
- 如图二所示，左上角存在 “L” 型，在 “L” 型中找出互相垂直的两条蓝边（是同一条边），两条蓝边的蓝点为公共点。这两条蓝边延伸出的两条红边是同一条边，因为两个蓝点是同一个点，且一条直线有两个点，所以两个红点也是同一个点。

（三）平移和旋转

基础知识之移面：当满足，那首尾两条边必然是同一条公共边，则两头的两个面，
基础知识之转面：当满足，则直角所对应的那两条边必然是同一条公共边，这两个面可以。转面要注意两点，一是某个面要去的方向与它自身旋转的方向一致；二是旋转度数为 90°。
注意：中心对称图形旋转两格，图形不变。对于非中心对称图形来说，是上下左右互换了。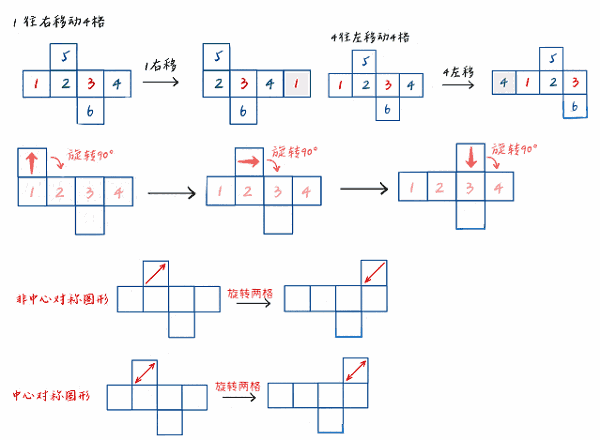

（四）解题方法

画边法
- 结合选项，找一个。
- 。注意：展开图和立体图都要画边 如下图所示，立体图的边 1 为 cb 的公共边，而展开图的边 1 为 ce 的公共边，面不一致，可以排除该选项。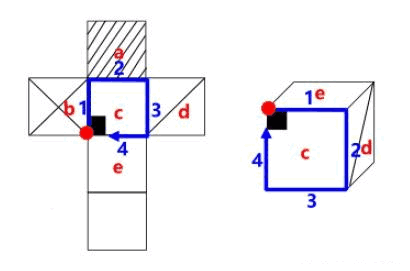
- 最后在展开图和立体图一一进行匹配，。
箭头法
- 原理：在一个平面中我们知道可以用一根箭头来表示方向，同样的，在空间中任何方向也都可以用箭头在立体的维度中展现，由于箭头是有方向的，面和面组成体，因此在立体图形中箭头上下左右所对应的图形的样式即使做任何翻折是不会发生任何改变的，借助面上的箭头方向可以来对应排除。
- 箭头法做题步骤：
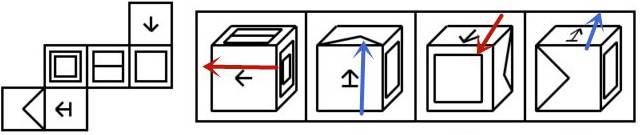
  ①选项图形找基准面画箭头（如下图选项 A 的箭头）
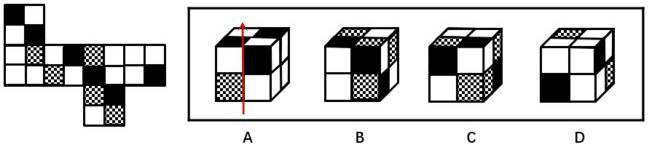
  ②题干图形画对应面上的箭头（如下图所示）
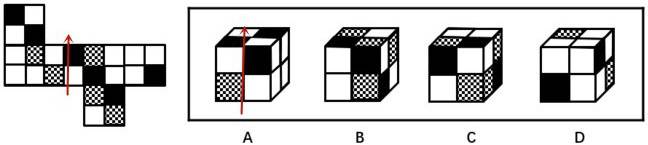
  ③依据箭头判断正确与否（如下图所示），对应图形箭头的右面（红三角）的图形非相同图形，箭头上面的完全相同，因为有不同，所以排除选项 A，其他选项类似排除。
- 基准面的选用原则：
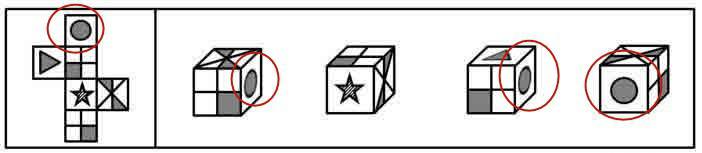
  ①原则：题干图形出现最多的面。
  ②原则：非对称的特殊面（对称图形画箭头至少两次，浪费时间），红色圈内的图形是对称图形，画箭头各个角度没差别，这个时候即使出现很多次也不可能选择这种。
- 总结：就是先在展开的平面图中找到一组相同的面做标记，再看图形样式位置是否完全一致来进行选项的排除。
马走日法
- 定义：马走日法跟象棋中的 “马” 走法一样，先找到一个某点，通过可以找到另一个公共点，那么这两个点为公共点，直到把公共点连接的三个面找出来。 例 1：点 A -> 点 1，马走日第一次，点 1 -> 点 B，马走日第两次得到 A、B 为公共点，此时只能确定两个面，需要找到第三个面，继续使用马走日法，点 B -> 点 1 -> 点 C 或者点 A -> 点 1 -> 点 C，因此公共点为 ABC 连接的三个面为绿色面。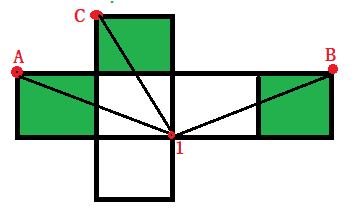
例 2：点 b -> 点 1 -> 点 B，所以 b 点和 B 点为公共点，B 点连接了两个面，公共点连接的三个面为蓝色+红色的面已经找到了，因此不需要使用马走日法了。同理点 a 和点 A 为公共点。点 a 连接了两个面，公共点连接的三个面为黄色+红色的面。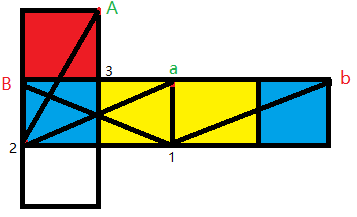
- 注意：马走日法是为了找到 3 个公共点，马走日要灵活运用。例 1 中走了 4 次“日”，例 2 中走了两次“日”；例 2 图中的点 3 就不需要走“日”，因为本身点连接了 3 个面。

二、四面体

四面体的展开图要么是三角形，要么是平行四边形。四面体的四个面都相邻，不存在相对面不能使用相对面排除法，直接使用。

四面体的展开图中，如何判定公共边?

方法一：构成一条直线的两条边是公共边。例如图①和图②中，1 边和 2 边是公共边。
方法二：平行四边形展开图中，两端的短边是公共边。例如图②中，5 边和 6 边是公共边。
方法三：四面体同样可以使用画边法

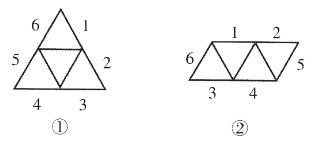
四面体公共边判定

三、立体拼合

题型判定：
- 提问：题干中完整图形是由残缺图形与哪个选项共同构成？
- 题干：给出一个完整图形及几个残缺图形
解题方法：
- 数个数（选项个数是否与题干一致）
  例：（2019 国家）下图为同样大小的正方体堆叠而成的多面体正视图和后视图。该多面体可拆分为①、②、③和④共 4 个多面体的组合，问下列哪一项能填入问号处？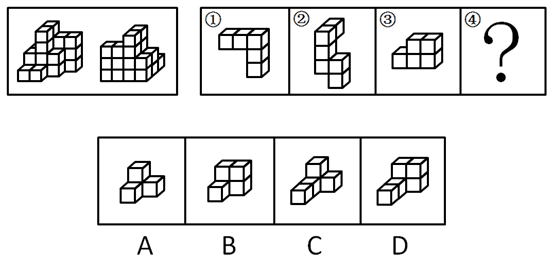
  解析：图形可分为前中后 3 排，最前面一排，根据正视图可知共有 2 个小立方体，中间一排，根据正视图和后视图可知共有 8 个小立方体，最后一排，根据后视图可知共有 12 个小立方体，故该多面体共有 2+8+12=22 个小立方体。观察题干图形发现，①有 5 个小立方体，②有 6 个小立方体，③有 5 个小立方体，所以若要将①、②、③、④组合在一起拼成题干多面体，则④应该有 6 个小立方体。A 项有 4 个小立方体，B 项有 5 个小立方体，C 项有 5 个小立方体，D 项有 6 个小立方体。故正确答案为 D。
- 试拼（找特殊块->“占地大”的）
  例：（2021 国家）左图给定的是由相同正方体堆叠成的多面体的正视图和后视图。该多面体可以由①、②和③三个多面体组合而成，问以下哪一项能填入问号处？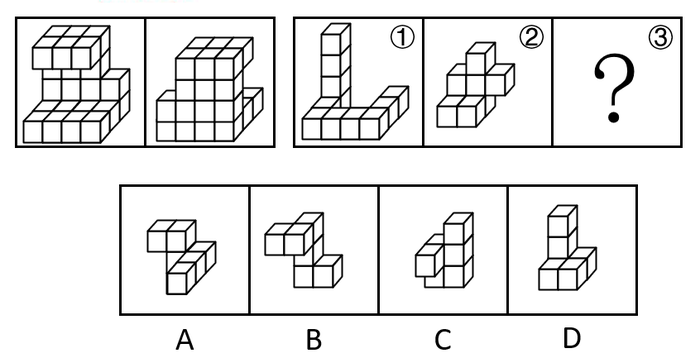
  解析：观察题干，母图一共 4 层，图①横跨了所有的层级，并且图①可以直接拼上去，没有第二种拼法，所以我们用先试拼，把图①拼上去。如下图所示
  对于图②最底下的一层有 4 个方块。在上图当中最底层刚好有四个格子，图②第二层 3 个方块也与上图倒数第二层缺 3 块对应，可以直接拼上去，如下图所示。
  剩下的就剩第一层五个方块，第二层的一个方块，对应的是 C 选项
- 分层画图法（化立体为平面，化拼为拆）
  例：（2022 国家）左图给定的是由相同正方体堆叠而成的多面体。该多面体可以由①、②和③三个多面体组合而成，以下哪项能填入问号处？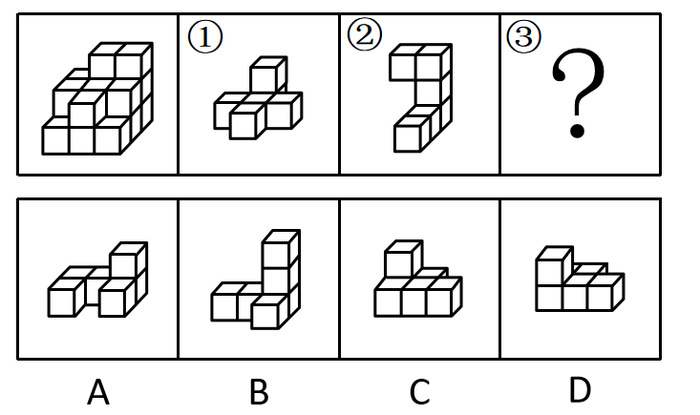
  解析：使用分层画图法要把每层的平面图画出来，如下图所示：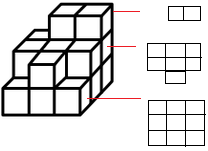
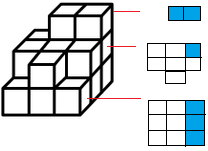
  首先，根据试拼的原理，先去考虑横跨层级多的图，把每一层的情况占据的位置在平面图中记录下来（打叉或画阴影）。优先看图②，横跨了三个层级，最底面占据 3 个位置，并且放在母图的最右侧。第二层占据一个位置，第三层占据 2 个位置，把平面图全部占据了。如下图所示
  然后观察图①，图①底层是一个十字架，明显在母图的底层平面图放不下，只能出现在母图二层平面图。而图①第一层剩下一个，如果放在母图平面图第一层是放不下的，所以要旋转放到母图倒数层平面图，有两种旋转方式，第一种左右旋转 180 度，及对应平面图的 A 位置，第二钟前后旋转 180 度，及对应平面图的 B 位置，并标记，如下图所示
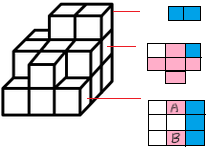
  假设放在 A 位置，平面图剩 5 个位置，观察选项，5 个位置组成的图像明显不存在。因此放在 B 位置。并且母图第二层平面图剩一个位置，观察选项及位置关系，只有 D 符合

四、平面拼合

做题原则：
- 图形在拼合时，各图形只可以平移，不能旋转、翻转。
- 平行等长消去，即平行且等长的两条边进行拼合，拼合之后线条抵消，当然如果没有别的线条与之平行，拼合后一定会保留下来。
做题方法：
- 优先找唯一方向（没有与之平行等长）的横线、竖线、斜线，此线一定在正确答案中出现，如果不出现则可以排除。
- 当题干中的小图形相同或者相似时，直接在选项中画出几个图形。

五、三视图

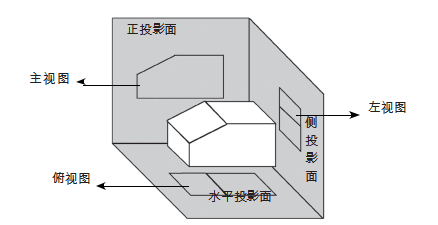
定义：三视图指的是立体图形的正视图、俯视图和侧视图。出题人不一定会严格按照三视图角度来考查，可能出现右视图（从右向左）和仰视图（从下向上）等，要具体情况具体分析。
- 正视图是指从物体的正面观察，物体的影像投影在背后的投影面上，这个投影影像称为正视图；
- 俯视图是指由物体上方向下作正投影得到的视图，也叫顶视图；
- 侧视图是指从物体的左面向右面或右面向左面正投影得到的投影图。
解题思维
- 所有的三视图都是平面图。若选项中出现立体图形，则一定错误。
- 原图有线就有线，原图没线就没线。
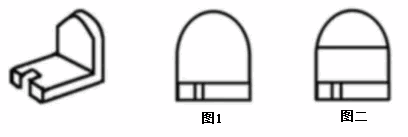
  如上图所示，图 1 和图 2 都是立体图形从左前方往右后方观察的，立体图形上方内部明显无横线，所以三视图也应无横线，图 1 正确，图 2 错误。
- 当被遮挡住时，看不见被遮挡部分。
  如上图所示，图 1、图 2 以及图 3 都是从立体图形左前方往右后方观察的，需要分两种情况进行讨论：①若只有图 1 和图 2，得出的应是图 1，因为后面的矩形应被前方的图形遮挡，被遮挡的部分应用虚线表示；②若只有图 2 和图 3，得出的应是图 3，被遮挡的部分用虚线表示最严谨，若没有用虚线表示，则被遮挡的部分应不画出来。
- 有些角度下弧会被压平。
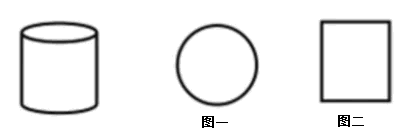
  如上图所示，图 1 是圆柱体的俯视图，图 2 是圆柱体的主视图、左视图以及右视图。
注意：三视图中被遮挡的部分是否应画虚线，需要从题干已知图形进行判断，与题干已知图形保持一致即可。
扩展（任一角度看）：三视图中正视图一般是前往后看，俯视图一般是上往下看，侧视图一般是左往右看或右往左看，这些是最常见的角度。但有时候会考察从任一角度看，那么此时你要多角度观察（优先观察三视图）。

六、截面图

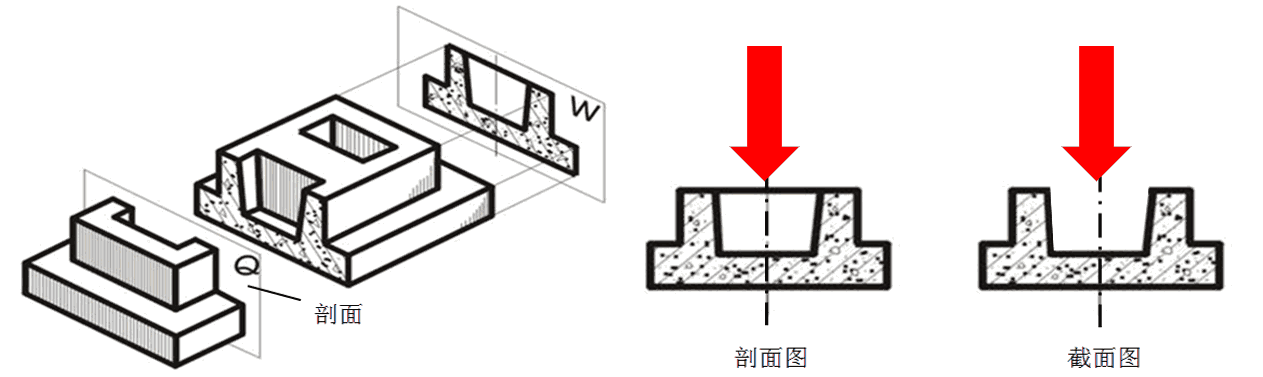
截面图是什么：用一个面(或一把无穷大的“刀”)将物体切开，被切部分的形状，也可以称为切面。
切的原则：① ；② 。
注意：截面和剖面不一样。剖面图是用一个面将物体剖开，对该部分的正投影图。
- 正、长方体
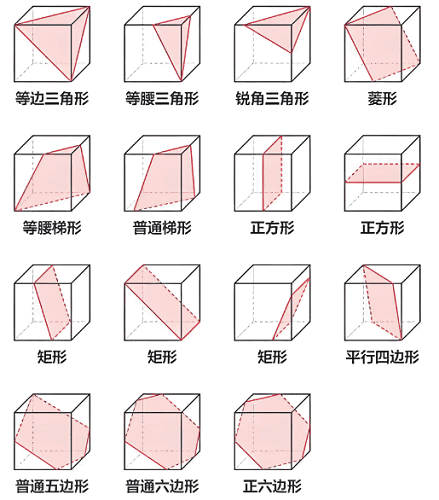
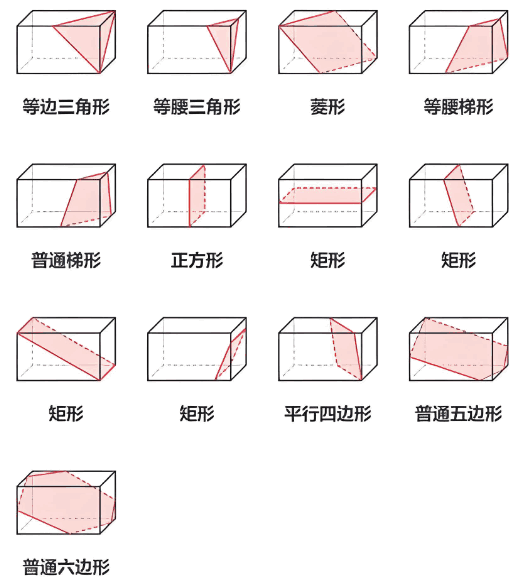
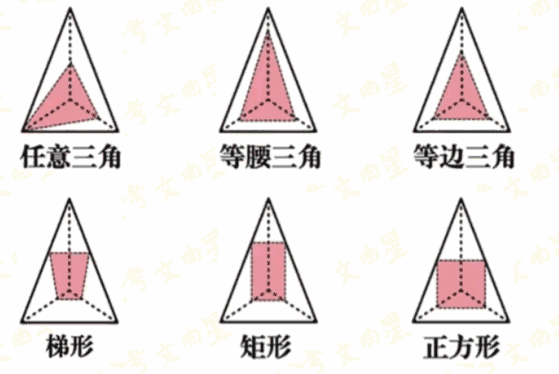
  注：正、长方体都截不出：钝角三角形、直角三角形、正五边形、六边形以上图形。
- 三棱柱
- 圆锥
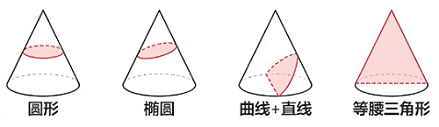
- 圆柱
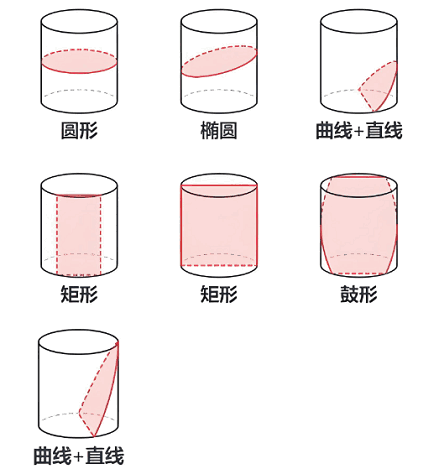
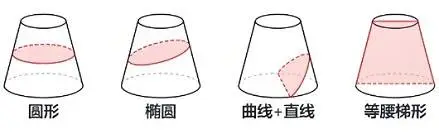
  注：圆柱截不出：梯形。
- 圆台
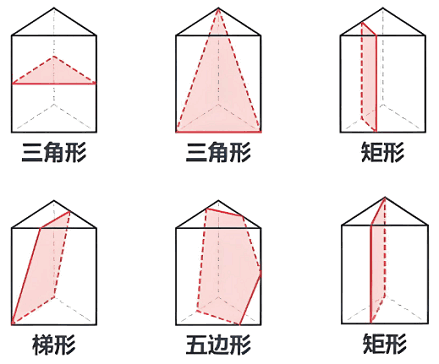
- 三棱锥
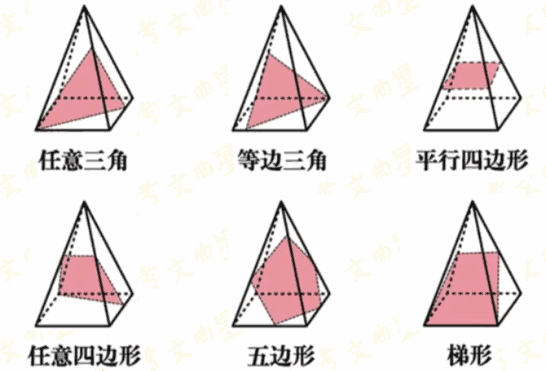
- 四棱锥
注意要点
- 六面体只能截出锐角三角形。
- 圆柱体无法截出梯形。
- 斜切过曲面必有曲线。
- 三视图基本 100%能截出。
- 圆柱切不出半圆。
- 内部挖空部分带实线；镂空部分不能有实线。
- 正四棱锥截不出长方形。
- 圆柱、圆锥、圆台横着切均是“圆”，斜着切均是“椭圆”。需要特别注意的是圆柱从上向下斜着切两侧是曲线，而不是直线。