Appearance
组合排列
🌐 10315 字 ⌛ 39 分钟
如果参加的是国考,尤其是考行政执法类或地市级,在组合排列题型里面,会有一种题是前面给出一则材料,后面给出 5 道小题,即“一拖五”,类似资料分析,除此之外,国考和省考基本没有区别。
题目特征:题目给出一组对象(如赵、钱、孙、李),并给出对象所具有的若干信息(如年龄性别、职业、身高、专业等),需要对各类信息进行匹配。
一、解题技巧
排除法:根据已知条件直接排除错误选项。
代入法:将选项代入已知条件中,验证是否正确。
- 。
- 当代入法做题时,如果某个选项符合条件,可直接选择该项,无需再验证其他选项。
辅助技巧:
- 最大信息:。
- 假设法:题干没有明确推理起点,且代入复杂,考虑假设。
- 画表法:遇到排序类问题可以画一维表,涉及到大小比较的时候,可以用符号(>、<、=)将信息表示出来;遇到两组以上对象,且无法排除代入类问题可以画二维表。
例:(2018江苏宜兴事业单位)
在一次国际会议上,来自四个国家的五位代表被安排坐在一张圆桌旁,为了使他们能够自由交谈,事先了解到情况如下:甲是中国人,还会说英语;乙是德国人,还会说汉语;丙是英国人,还会说法语;丁是日本人,还会说法语;戊是日本人,还会说德语。请问如何安排?
A. 甲 丙 戊 乙 丁
B. 甲 丁 丙 乙 戊
C. 甲 乙 丙 丁 戊
D. 甲 丙 丁 戊 乙
详解
解析内容
例:(2020江苏)
某医院护士小娟从抗疫前线胜利归来,单位同事小红、小丽和小明三人结伴来看望她。他们送给小娟一束鲜花及一些慰问品。小娟问这些礼物是谁买的?三人笑着回答:
小红:我没有买,小丽也没有买;
小丽:我没有买,小明也没有买;
小明:我没有买,是她们两人共同买的。
后来小娟得知,他们三人每人说的话都是一半对、一半错。 根据上述信息,可以得出以下哪项?( )
A.礼物是小红买的 B.礼物是小丽买的
C.礼物是小明买的 D.礼物是三人共同买的
详解
解析内容
例:(2017江苏事业单位)
某政务服务中心一楼有公安、民政、人社和卫计共4个服务窗口,现计划按照业务量由多到少调整窗口的顺序。已知,调整前各窗口业务量如下:
1 号窗口比民政窗口多;
3 号窗口比2号窗口少;
卫计窗口比公安窗口多;
人社窗口比民政窗口少。
卫计窗口不是 3 号窗口就是 4 号窗口。 据此,以下哪一项一定为真?
A. 公安窗口不是业务量最少的
B. 卫计窗口不是业务量最多的
C. 人社窗口应该从4号调整到3号
D. 民政窗口应该从3号调整到2号
详解
解析内容
例:(2016江苏公务员)
某单位工会成立职工业余兴趣活动小组,分台球、乒乓球、羽毛球、登山四个小组。已知该单位的甲、乙、丙、丁、戊、己、庚等7人每人各参加其中的两个小组,每个小组最少有其中的两人参加。最多有其中的5人参加。另外,还知道:
(1)丁与戊的参加情况完全相同;
(2)己与庚的参加情况完全相同;
(3)如果甲参加台球组,则丁也会参加台球组;
(4)只有乙和丙参加乒乓球组。 如果登山组只有己和庚参加,则可以得出以下哪项?
A.甲参加台球组,羽毛球组
B.乙参加台球组,羽毛球组
C.己参加台球组,登山组
D.庚参加羽毛球组,登山组
详解
解析内容
例:(2019 河南)
某班分小组进行了摘草莓趣味比赛,甲、乙、丙 3 人分属3 个小组。3 人摘得的草莓数量情况如下:甲和属于第 3 小组的那位摘得的数量不一样,丙比属于第 1 小组的那位摘得少,3 人中第 3 小组的那位比乙摘得多。据此,将 3 人按摘得的草莓数量从多到少排列,正确的是:
A.甲、乙、丙 B.甲、丙、乙
C.乙、甲、丙 D.丙、甲、乙
详解
解析内容
例:(2021甘肃)
三位房东甲、乙、丙将自己的房子分别租给租客小李、小张、小王。甲说他租给的是小李;小李说他租的是丙的房子;丙说他租给的是小王。 若这三人均没有说真话,则下列选项正确的是:
A.房东乙将房子租给了小张
B.房东丙将房子租给了小李
C.小王租的是房东乙的房子
D.小李租的是房东乙的房子
详解
解析内容
二、特殊题型
只对一半题型
题型特征:说了两句话,只猜对了一半。
解题技巧:
- 代入法。
- 运用最小信息假设法(即出现次数最少的),假设出现次数最少为真,代入看能否满足一对一错,如果满足则假设成立。
秒杀技巧:。
例
甲、乙、丙三人大学毕业后选择从事各不相同的职业:教师、律师、工程师。其他同学做了如下猜测:
小李:甲是工程师,乙是教师。
小王:甲是教师,丙是工程师。
小方:甲是律师,乙是工程师。
后来证实,小李、小王和小方都只猜对了一半。 那么,甲、乙、丙分别从事何种职业?
A.甲是教师,乙是律师,丙是工程师
B.甲是工程师,乙是律师,丙是教师
C.甲是律师,乙是工程师,丙是教师
D.甲是律师,乙是教师,丙是工程师
详解
解析内容
例
阿根廷大学的一位老师让五位留学生看校史上的五位大数学家的画像,让每位学生任意挑选两幅画像说出名字。
张说:“2号是高斯,3号是黎曼。”
倪说:“1号是希尔伯特,2号是闵可夫斯基。”
朱说:“3号是闵可夫斯基,5号是希尔伯特。”
韦说:“2号是高斯,4号是外尔。”
方说:“4号是外尔,1号是黎曼。” 老师发现每位学生都只说对了一半,那么1号画像是______。 A.黎曼
B.闵可夫斯基
C.希尔伯特
D.高斯
详解
解析内容
点名题型
条件:只有某某或某特征的人说的是真话
秒杀技巧:题干里某特征句里提到的人且说的话都为假
例:(2021江苏)
甲、乙、丙、丁4位中学同学毕业30年后相聚。现在,他们已成为企业家、大学教师、歌手和会计师,且每人只有一种身份,并不重复。他们在中学时代就各人的未来职业有过如下预言:
甲:乙不会成为歌手;
乙:丙会成为会计师;
丙:丁不会成为企业家;
丁:乙不会成为大学教师。 现在看来,他们当中只有会计师的预言是正确的。 根据上述信息可以推断,甲、乙、丙、丁的职业分别是:
A.企业家、大学教师、歌手、会计师
B.大学教师、歌手、企业家、会计师
C.企业家、歌手、会计师、大学教师
D.会计师、大学教师、歌手、企业家
详解
解析内容
例:(2017江西)
有四个人,他们分别是小偷、强盗、法官、警察。第一个人说:“第二个人不是小偷。”第二个人说:“第三个是警察。”第三个人说:“第四个人不是法官。”第四个人说:“我不是警察,而且除我之外只有警察会说实话。” 如果第四个人说的是实话,那么以下说法正确的是:
A.第一个人是警察,第二个人是小偷
B.第一个人是小偷,第四个人是法官
C.第三个人是警察,第四个人是法官
D.第二个人是强盗,第三个人是小偷
详解
解析内容
"3+2" + "4+3"题型
什么是"3+2" + "4+3"题型:具体来说,如果有5个人,可以分成3人和2人两组,3人和2人之间差1。如果有7个人,则可以分成4人和3人两组,4人和3人之间也差1。
秒杀技巧:
- 找相同:首先,找出题干中相同条件的人,将他们归为一组。
- 做排除:根据题目中的条件,排除不符合要求的人。
例:(2018辽宁)
某校招聘专任教师时有张强、李颖、王丹、赵雷、钱萍5名博士应聘。3人毕业于美国高校,2人毕业于英国高校;2人发表过SSCI论文,3人没有发表过SSCI论文。 已知,张强和王丹毕业院校所在国家相同,而赵雷和钱萍毕业院校所在国家不同;李颖和钱萍发表论文的情况相同,但王丹和赵雷发表论文的情况不同。最终,英国高校培养的一位发表过SSCI论文的博士被录取。 由此可以推出:
A.张强没发过SSCI论文
B.李颖发表过SSCI论文
C.王丹毕业于英国院校
D.赵雷毕业于英国院校
详解
解析内容
例:(2010江苏)
N中学在进行高考免试学生的推荐时,共有甲、乙、丙、丁、戊、己、庚等7位同学入围。在7人中,有3位同学是女生,4位同学是男生,有4位同学的年龄为18岁,而另3位同学年龄则为17岁。已知,甲、丙和戊年龄相同,而乙、庚的年龄则不相同;乙、丁与己的性别相同,而甲与庚的性别则不相同。最后,只有一位17岁的女生得到推荐资格。 据此,可以推出获得推荐资格的是:
A.庚
B.戊
C.乙
D.甲
详解
解析内容
4+3+2+1题型
什么是4+3+2+1题型:有4个人,对应3个条件,其中一个条件有三个人满足,另一个条件2个人满足,最后一个条件1个人满足,即满足每个条件的人数分别为3、2、1,这就是“3+2+1”。
解题技巧:
第一步:用3找出不同的人。即根据“一个条件有三个人满足”,找到不满足条件的人。
第二步:用2找到不同的人的队友。结合“一个条件有两个人满足”,找到“不同的人”的队友。
第三步:队友就是正确答案,选答案。
例:(2017天津)
合格的教师应该具备三个条件:第一要有责任心;第二要有丰富的知识;第三要有一定的管理水平。现有至少符合条件之一的甲、乙、丙、丁四位大学毕业生报名竞争一个教师岗位,其中一人合格,已知:
(1)甲、乙管理水平相当;
(2)乙、丙都有责任心;
(3)丙、丁并非都有责任心;
(4)四人中三个人责任心强、两人管理能力突出、一人知识丰富。 那么能够胜出的一位是:
A.丙
B.丁
C.甲
D.乙
详解
解析内容
例:(2022江苏)
某高校选派甲、乙、丙、丁4位专家组成乡村振兴调研小组,担任组长的专家为男性、党员、教授。已知这4位专家中:
(1)每位专家都至少具有组长的一个特征;
(2)有党员3人,男性2人,教授1人;
(3)甲和乙性别相同;
(4)乙是党员当且仅当丙是党员;
(5)丙和丁不全是党员。 由此推出,担任组长的是:
A.甲
B.乙
C.丙
D.丁
详解
解析内容
矛盾大小比较
题型识别:A>B,C>D
答案:选择AC > BD
例如:男生人数多于女生人数,北京多于上海。那么北京男生 > 上海女生
例:(2015广东)
某高中只有文科班和理科班,男生人数比女生多,理科班人数比文科班多。 根据以上条件,可以判断下列说法必定为真的是:
A.文科班的男生总人数多于文科班的女生总人数
B.理科班的男生总人数多于理科班的女生总人数
C.文科班的男生总人数多于理科班的女生总人数
D.理科班的男生总人数多于文科班的女生总人数
详解
解析内容
例:(2020上海)
某三甲医院的医生中,专科医院毕业的医生人数大于非专科医院毕业的医生人数,女医生的人数大于男医生的人数。 如果上述论述是真的,那么_____项关于该医院医生的断定也一定是真的。
(1)非专科医院毕业的女医生人数大于专科医院毕业的男医生人数。
(2)专科医院毕业的男医生人数大于非专科医院毕业的男医生人数。
(3)专科医院毕业的女医生人数大于非专科医院毕业的男医生人数。
A.(1)和(2) B.只有(2)
C.只有(3) D.(2)和(3)
详解
解析内容
圆桌问题
题型特征:出现圆形,考查座位排列或信息匹配,难度较大。
解题技巧:先画出圆桌,圆桌和表格一样,都是辅助工具。注意左右顺序,直线排列时,所有人都面向同一方向落座,左右方向很容易判断,而一群人围坐在圆桌时,所有人是面向桌子中心落座,此时左右方向就是我们非常容易混淆弄错的。
以下图为例,四个人围桌而坐,均面向桌子,在这种简单情况下,我们可以很轻松地知道,甲的左手边是乙,右手边是丁;丙的左手边是丁,右手边是乙。归纳规律之后,我们发现,每个人的顺时针方向为左手边,逆时针方向为右手边。因此,在圆桌上分不清左右的时候,我们只需要画个简单的时针箭头就能快速分清方向了。
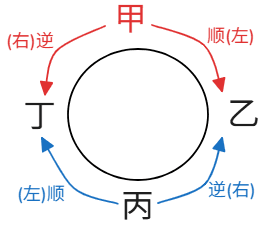
例:(2014四川)
某开发区发展委员会召开环境工作专题圆桌会议,参加会议的有委员会主任和副主任,以及委员会所属的开发区环保局、工业局和农业局的局长和副局长。他们八个人均匀地坐在一张会议圆桌旁,只有一个同部门的正职和副职的座位被分隔开了。并且:
(1)委员会副主任对面的人是坐在环保局局长左边的一位局长;
(2)工业局副局长左边的人是坐在农业局局长对面的一位副局长;
(3)农业局局长右边的人是一位副局长,这位副局长坐在委员会主任左边第二个位置上的副局长的对面。 则座位一定被隔开的是:
A.环保局的局长和副局长
B.工业局的局长和副局长
C.农业局的局长和副局长
D.委员会的主任和副主任
详解
解析内容
例:(2018国家)
某次会议讨论期间,甲、乙、丙、丁、戊被安排在一张圆桌前进行讨论,圆桌边放着标有1~5号的五张座椅(未必按序排列)。实际讨论时,甲、乙、丙、丁、戊5人均未按顺序坐在1~5号的座椅上,已知:
(1)甲坐在1号座椅右边第二张座椅上;
(2)乙坐在5号座椅左边第二张座椅上;
(3)丙坐在3号座椅左边第一张座椅上;
(4)丁坐在2号座椅左边第一张座椅上。 如果丙坐在1号座椅上,则可知甲坐的是哪个座椅?
A.2号 B.3号
C.4号 D.5号
详解
解析内容
材料题型
- 题型特征:一段材料,多个问题;此类题型较难,技巧性低,并且耗时。国考(一拖五)、江苏等会考。
- 题型分类:
- 分组:通常题干给出一些主体和信息,根据一定的推理,将各主体与对应的信息匹配。
- 排序:题干也给出一些主体和信息,按照一定的顺序标准将各主体进行排列,比如时间先后顺序、年龄大小、奖项前后等。
- 注意:
- 推出条件,最重要,每题几乎都要用到。正反结论均要推出,可以把所有推出条件写一旁。可以利用推出条件正向假设或者逆向假设。
- 此类题型通常只剩余2个位置,互相组合。如果不是,按条件给出的可能性分类讨论即可。
例:(2025国考)
某科研机构今年拟举办甲、乙、丙、丁、戊、己、庚、辛8次学术会议,每个季度最多举办3次,且各次会议举办时间不重叠。具体安排要求如下:
(1)丁、辛安排在第二季度;
(2)甲、戊安排在同一个季度;
(3)丁在乙之后丙之前举办;
(4)丙在甲之前己之后举办。
1.下列哪2次会议可以安排在第一季度?
A.甲和戊 B.丙和丁
C.丁和己 D.己和庚
2.如果第二季度只安排2次会议,那么以下哪次会议一定安排在第一季度?
A.甲
B.乙
C.庚
D.丙
3.如果丙、戊安排在第四季度,下列哪2次会议可以安排在第三季度?
A.甲和庚 B.乙和丁
C.乙和己 D.己和庚
4.如果每个季度至少安排1次会议,并且最后一个季度仅安排1次会议,下列哪2次会议一定安排在第三季度?
A.甲和戊 B.乙和丙
C.丙和己 D.己和庚
5.如果甲安排在第三季度,第四季度不安排会议,庚不可能和哪次会议安排在同一个季度?
A.乙 B.丙
C.己 D.辛
详解
解析内容
